Finite Automata and Regular Expressions

An automaton is a specification for a symbol processing machine. You can think of it as a machine which matches some expression to some input piece of text or sequence of events. It will tell you either yes, this matches, or no, it does not. Text, for example, is made up of symbols, in this case we usually talk about individual characters. Note that we don't have to be talking about text, but it's easier to explain and apply if we do. Our machine has states, which represents some possible internal condition of the machine. A finite automata has a finite number of these states. We label these internal states with things like q₀,q₁,...,q_n, paying no mind to what the actual internal state means. We only care about what conditions are necessary to move from one state to another.

We draw this using a state transition diagram to make it easier to understand what one of these machines does. These diagrams are made up of states drawn as circles, and transitions, drawn as labeled directed arcs between the circles. One of these circles is the start state. It is usually drawn as a circle with an arc coming into it, and the arc comes out of no other arc. It is also usually labeled q₀. An accepting state is drawn as a double circle - it is the goal that we reach this state.

Now we can describe how one of these automatons works. The machine looks at the input symbol by symbol, following the arcs out of the circle (state) it currently occupies to the one the arc points to. The input is valid (or said to be in the language of the machine) if the input has been entirely consumed, and the machine is in an accepting state. Otherwise, the input is not in the language.

We'll motivate some examples by thinking about a soda machine. Consider a soda machine which accepts dimes and nickles. Cans of soda cost 15 cents. See this page for the example: source.

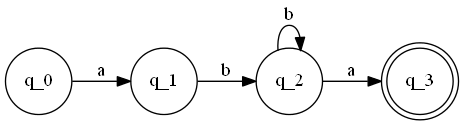
Let's look at a few text examples. Our first has 4 states - q₀,q₁,q₂,q₃. The start state is q₀ as usual, and the accepting stae is q₃. The symbols in the language are a and b. The transitions are shown in the below diagram:

As you can see, this machine only accepts after having seen the string "aba". We can modify this machine to accept on "aba" but also "abbbbbbba" for any number of b's greater than or equal to 1. This actually accepts an infinite number of "words!"

That's the basic idea - we just follow the path of the arrows for each character we read in a string, and if we find ourselves in an accepting state when we're done, then we accept the string, otherwise we do not.

In-Class Exercise: What words does the below automata accept?

Note: The definition supplied here is rather informal. More formally a finite automaton is defined as a 5-tuple (Q, Σ, q₀, δ, A) where Q is the set of states, Σ is the set of symbols, q₀ is the start state, A is the set of accepting states, and δ is the set of transitions.

This will be the first "formal language" that we will learn! We're going to look at regular expressions as they are defined in Microsoft Word. Note, to use them yourself, follow this guide.

Regular expressions are used to find text matching certain patterns in a document. They represent a regular language. That means that there exists a finite automaton which as the same language. A regular expression is really just a shorthand way of writing out the finite automaton you're interested in using.

They are quite powerful (as you see above!), and may change the way you use find and replace!

Let's start off easy: single character and multicharacter wildcards.

• The ? symbol represents a wildcard for a single character. For example, if you search for
  d?g
  , you might find things like
  dog
  or
  dig
  . It will also match part of longer words, like
  dig
  ital.
• The *symbol means 0 or more single character wildcards. So if you searched for
  d*g
  , you would get
  dog
  and
  dig
  again, but also
  drag
  and "
  dorsal fin rig
  ". The pattern matching is lazy, meaning it will stop matching as soon as it can, but this may be several words away!

In-Class Exercise: I want to match the words intense and incense, what expression might I use?

Let's say we want to find the words and , but not or . We need a way to say we want one or more letter "o". To do this we can use the @, producing the following find query: . You can use curley brackets to specify a certain number of the previous letter. For example, matches but not or (??).

We still have a problem though. These expressions match parts of the word chosen for example. We'd like to be able to say where the start and end of the word is, which we can do using < and > around our query. Note though, that this can produce undesired results - it doesn't stop there from being other spaces in between! You can use these individually, or in pairs.

Square brackets, [ and ], are used in pairs to represent possible values for a single letter. For example, [abc] matches a, b, or c. Ranges can be used. For example, [A-Z] finds any uppercase letter, and [0-9] finds any digit. [0-9A-z] finds any digit or letter. This can be used in combination with !, the negation symbol. Saying [!A-Z] finds anything that isn't a capital letter. This brings up an issue though! What if I want to search for [!] ?... Well, to do this, you must use the escape character, which is a backslash, "\". So to search for [!] what you really mean is [\!]. This must be done for any of the special characters:  ( [ ] { } < > ( ) - @ ? ! * \ ).

Example: To find any number, we might use <[0-9]@>, meaning one or more instances of a digit, which are both the start and end of a word.

In-Class Exercise: How would we match a telephone number?

For further explanation of these, see the Word MVP document about using wildcards. They have a helpful zen tip on that page too: "when using wildcard searches: don't wrinkle your brow or bite on your tongue while thinking it through – you have to keep up a regular expression. :-| "