Microproject
Suppose there is a 4×4 grid. Write an ASP program to show the cell (1,2) and all the cells within the distance of 2 of (1,2).
Main Project: Social Distancing Simulator
You’re trying really hard to adhere to social distancing rules, but sometimes your visits to the local park aren’t so easy. You’re trying to get from a point on the south side of the park to a nice patch of grass on the north side. There are several people around and sometimes they aren’t trying as hard as you to do the right thing. But you’ve had a great idea! You launch a drone and create a map of the current location of all of the people in the park. Now you just have to write a little program to find a path such that you stay 6 feet away from every other park-goer!
In order to simplify the problem somewhat you divide the part of the park you need to traverse into a 25×25 grid, where each square is 1 foot by 1 foot. You only worry about moving north, east, or west (no looping back to the south). You decide to measure the 6-foot distance from the center of each square using the Pythagorean theorem. Therefore, [0,0] and [0,6] are 6 feet apart, while [0,0] and [4,3] are only 5 feet separated.
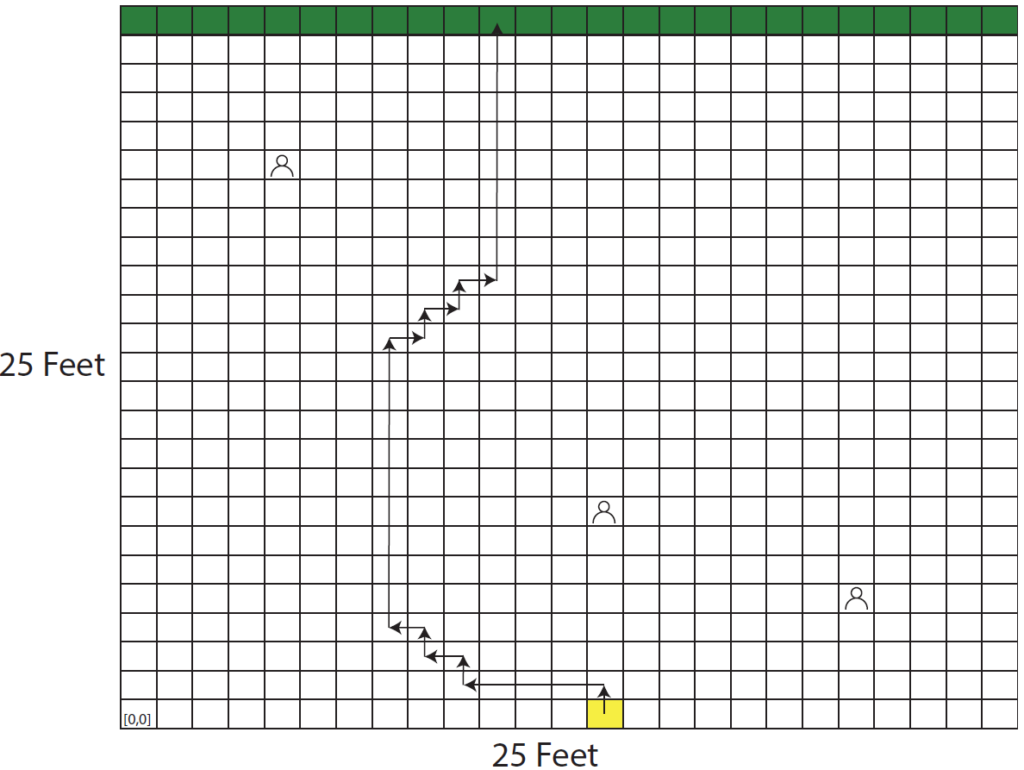
Above is a sample configuration of the park. It is possible different positions on the south side of the park might be specified, and the other park-goers might be in different places. The path shown is simply the first path my solution produced – yours may do something different!
In ASP you will create a program which automatically finds and outputs a path through the park, given a starting position on the south edge of the park, the size of the park, the goal Y coordinate, and the positions of any other people in the park.
|
1 2 3 4 5 6 7 8 9 10 11 12 |
The solution is represented by atoms of predicate path/4: path(X1,Y1,X2,Y2). % the path has an edge between the cells (X1,Y1) and (X2,Y2) For instance, the solution of the example consists of the following atoms: path(13,0,13,1) path(13,1,12,1) path(12,1,11,1) path(11,1,10,1) path(10,1,9,1) path(9,1,9,2) path(9,2,8,2) path(8,2,8,3) path(8,3,7,3) path(7,3,7,4) path(7,4,7,5) path(7,5,7,6)path(7,6,7,7) path(7,7,7,8) path(7,8,7,9) path(7,9,7,10) path(7,10,7,11) path(7,11,7,12)path(7,12,7,13) path(7,13,8,13) path(8,13,8,14) path(8,14,9,14) path(9,14,9,15) path(9,15,10,15) path(10,15,10,16) path(10,16,10,17) path(10,17,10,18) path(10,18,10,19) path(10,19,10,20)path(10,20,10,21) path(10,21,10,22) path(10,22,10,23) path(10,23,10,24) |
Representation Hints
Below are some hints for representation, you don’t need to use all of these (except for path), but you may wish to.
Constants:
- n1 is the length of the side
- n2 is the distance between the south edge and north edge
- startX is the X-coordinate of the starting position
- d is the required social distance
Predicates:
- p(X,Y) represents the person at (X,Y)
- path(X1,Y1,X2,Y2) is the path has an edge between the cells (X1,Y1) and (X2,Y2)
You may wish to start with a smaller grid. Perhaps with setup as follows:
|
1 2 3 4 5 6 7 8 |
#const n1=3. #const n2=3. #const startX=1. #const d = 2. p(1,2). %answer:path(1,0,2,0) path(2,0,3,0) path(3,0,3,1) path(3,1,3,2) path(3,2,3,3) |