Programming Challenge 4: Nonrepresentational Artistic Expressions

Overview

Your task is to write several separate Java programs for this assignment, all but one in the context of the Nonrepresentational Painting World (NPW). These programs, with the one exception, will make use of both the painter functionality and the shapes functionality of the world. You will be asked to place each of these programs, including the one exception, in the npw package of your CS1 project.

Why do it?

By composing Java solutions to these non-representational artistic expression problems you will:

Gain considerable practice in creating and using objects.
Gain considerable practice in reading and understanding programs written by others.
Gain considerable practice in program modification.
Practice using selection and repetition constructs.
Further explore the notion of creativity from constraint in the course of microworld problem solving.

The Entrance

You should review the Nonrepresentational Painting World functionality, and the mechanisms for selection and repetition previously presented in lecture and in lab. You might also like to adopt a frame of mind in which laying down shapes in the plane resonates with nonrepresentational art. Perhaps you would like to Google Klee, Stella, Hirst, and a number of other modern artists, in order to explore some of their images and ideas.

Problem 1: The Cave

There is a style of top-down video game where you move through progressively narrowing, winding caves. This style of game first appeared as a text-based game. In this problem you’re going to generate a piece of a map for one of these games. If you don’t like that kind of thing, you can think of this as just generating a nice little text-based image.

Write a program called CaveMap in your npw package that will (1) accept, from the standard input stream, data corresponding to the width of the map, and the width of the cave, and (2) print, to the standard output stream, the map made of stars to represent a wall, and white space to represent the cave. Your program should be consistent with the following set of three demos:

run:
Enter the width of the game map: 8
Enter the width of the cave (must be less than the game map width): 5
     ***
*     **
**     *
***     
**     *
*     **
     ***

Enter the width of the game map: 10
Enter the width of the cave (must be less than the game map width): 4
    ******
*    *****
**    ****
***    ***
****    **
*****    *
******    
*****    *
****    **
***    ***
**    ****
*    *****
    ******

Enter the width of the game map: 5
Enter the width of the cave (must be less than the game map width): 1
 ****
* ***
** **
*** *
**** 
*** *
** **
* ***
 ****

run:

Enter the width of the game map: 8

Enter the width of the cave (must be less than the game map width): 5

***

* **

** *

***

** *

* **

***

Enter the width of the game map: 10

Enter the width of the cave (must be less than the game map width): 4

******

* *****

** ****

*** ***

**** **

***** *

******

***** *

**** **

*** ***

** ****

* *****

******

Enter the width of the game map: 5

Enter the width of the cave (must be less than the game map width): 1

****

* ***

** **

*** *

****

*** *

** **

* ***

****

Moreover, your program should be consistent with the following Java program text. What we did was to write the program, and then delete the instructions within the main method, and the entire drawOneRow method. Your job is to add the instructions back. Or at least, instructions which will do the job. Other than adding instructions pertaining to these two methods, all of the executable code should remain exactly as in the accompanying program text. You should be able to use your program to generate the game maps that appear in my demo, and many others, as well.

/*
 * Program to draw a part of a map for a cave travelling game.
 * Game width and cave width are read from standard input.
 */
package npw;

import java.util.Scanner;

public class Cave {

    public static void main(String[] args) {
    }

    public static void drawMap(int caveWidth, int gameWidth){
        // Cave moving right...!
        for (int i = 0; i < gameWidth - caveWidth; i = i + 1){
            drawOneRow(i, caveWidth, gameWidth);
            System.out.println();
        }
        // Cave moving left...!
        for (int i = gameWidth - caveWidth; i >= 0; i = i - 1){
            drawOneRow(i, caveWidth, gameWidth);
            System.out.println();
        }
    }
}

* Program to draw a part of a map for a cave travelling game.

* Game width and cave width are read from standard input.

package npw;

import java.util.Scanner;

public class Cave {

public static void main(String[] args) {

}

public static void drawMap(int caveWidth, int gameWidth){

// Cave moving right...!

for (int i = 0; i < gameWidth - caveWidth; i = i + 1){

drawOneRow(i, caveWidth, gameWidth);

System.out.println();

}

// Cave moving left...!

for (int i = gameWidth - caveWidth; i >= 0; i = i - 1){

drawOneRow(i, caveWidth, gameWidth);

System.out.println();

}

Problem 2: Entropy

Write a program called Entropy in your npw package to paint a series of vertical columns, each with several diamonds in them, with the diamonds exhibiting more randomness in terms of rotation, size, and location as they move to the right. The width and height of the canvas, as well as the scale of the diamonds, should be read from dialog boxes. Actually, we have written this one for you. What we would like for you to do is enter it carefully (don’t copy/paste!), run it several times, and study it! It’s important that you understand how it works for later parts of this assignment.

/*
 * A program to paint an artistic representation of entropy in the NPW.
 */
package npw;

import painter.SPainter;
import shapes.SCircle;
import shapes.SSquare;

import javax.swing.*;
import java.awt.*;
import java.util.Scanner;

public class Entropy {

    private void paintTheImage(){

        // determine the canvas dimensions
        int canvasHeight = getNumber("Canvas height");
        int canvasWidth = getNumber("Canvas width");

        // set up a circle (imagining a sphere-packing problem :)
        //   and get the square inscribing the circle so that the lattice
        //   will be just perfect.
        int radius = getNumber("Diamond scale");
        SCircle invisibleCircle = new SCircle(radius);
        SSquare sq = invisibleCircle.inscribingSquare();

        // instantiate the painter and canvas
        SPainter cassatt = new SPainter("Entropy", canvasWidth, canvasHeight);

        // frame the canvas: we want a 10 unit frame of white on all sides.
        int frameDepth = 10;

        // compute the number of columns needed
        // working canvas width / diameter of invisibleCircle
        int totalNumberOfColumns = (int) ((canvasWidth-2*frameDepth)/invisibleCircle.diameter());

        // check the work and adjust horizontal frameDepth as needed.
        int horizFrameDepth = (int) ((canvasWidth - (totalNumberOfColumns * invisibleCircle.diameter())) / 2);

        // compute the number of squares needed per column
        int numberOfSquaresPerColumn = (int) ((canvasHeight - 2*frameDepth)/invisibleCircle.diameter());

        // check the work and adjust the vertical frameDepth as needed
        int vertFrameDepth = (int) ((canvasHeight - (numberOfSquaresPerColumn * invisibleCircle.diameter())) / 2);

        // move the painter to the top left of the working canvas area
        //    remember, painter began at center of canvas
        cassatt.mfd(0.5*canvasHeight-vertFrameDepth);
        cassatt.mlt(0.5*canvasWidth-horizFrameDepth);

        // center the painter over the first column
        cassatt.mrt(invisibleCircle.radius());

        // track the number of columns painted
        int colNumber = 0;

        // introduce a chaos factor to change things up
        double chaosFactor = 0;

        while (colNumber < totalNumberOfColumns){
            // set the color for the column
            cassatt.setColor(chooseColor());

            // paint a column
            paintOneColumn(cassatt,sq,numberOfSquaresPerColumn, chaosFactor);

            // center the painter over the next column
            cassatt.mrt(invisibleCircle.diameter());
            colNumber = colNumber + 1;
            chaosFactor = (1.0/totalNumberOfColumns)*colNumber;
        }
    }

    private Color chooseColor() {
        return Color.BLACK;
    }

    private void paintOneColumn(SPainter cassatt, SSquare sq, int numberOfSquaresPerColumn, double chaosFactor) {
        // move down enough to paint the first square
        cassatt.mbk(sq.diagonal()*0.5);

        // track the amount of distance travelled
        double distanceTraveled = sq.diagonal()*0.5;

        // track the number of squares that get painted in the column
        int squareNumber = 0;
        while(squareNumber < numberOfSquaresPerColumn){

            // paint a square, but as a diamond
            paintOneDiamond(cassatt,sq,chaosFactor);

            // move down
            cassatt.mbk(sq.diagonal());

            // track distance covered
            distanceTraveled = distanceTraveled + sq.diagonal();

            // track number of squares painted so far
            squareNumber = squareNumber + 1;
        }

        // make sure the painter is invariant wrt position
        cassatt.mfd(distanceTraveled);
    }

    private void paintOneDiamond(SPainter cassatt, SSquare sq, double chaosFactor) {

        // set the default values
        double origSquareSide = sq.side();
        double rotationOffset = 0;
        double offsetDirection = 0;
        double offsetDistance = 0;

        // when the chaosFactor is high enough, redefine the key values (sometimes)
        if (chaosFactor > 0.3){
            // flip the coin!
            double probability = Math.random();

            // for a heads, offset the diamond rotation a bit
            if (probability > 0.5){
                rotationOffset = (Math.random()*30)-15;
            }
        }

        if(chaosFactor > 0.5){
            // flip the coin!
            double probability = Math.random();

            // for a heads, change the size of the diamond a little bit
            if (probability > 0.5){
                double shrinkRate = (1 - probability)*0.7;
                sq.resetSide((int) ((1-shrinkRate)*origSquareSide));
            }
        }

        if (chaosFactor > 0.75){
            // flip a coin!
            double probability = Math.random();

            if (chaosFactor > 0.9){
                if (probability > 0.5){
                    offsetDirection = Math.random()*360;
                    offsetDistance = (Math.random()*(sq.diagonal()*0.5))*chaosFactor;
                }
            } else {

                // for a heads, paint the diamond off center
                if (probability > 0.5) {
                    offsetDirection = Math.random() * 360;
                    offsetDistance = (Math.random() * (sq.diagonal() * 0.5)) * 0.4;
                }
            }
        }

        // move the painter off center from the circle
        cassatt.tr(offsetDirection);
        cassatt.mfd(offsetDistance);
        cassatt.tl(offsetDirection);

        // rotate so that the square becomes a diamond
        cassatt.tr(45+rotationOffset);

        // paint
        cassatt.paint(sq);

        // rotate back!
        cassatt.tl(45+rotationOffset);

        // move the painter back to the center of the circle
        cassatt.tr(offsetDirection);
        cassatt.mbk(offsetDistance);
        cassatt.tl(offsetDirection);

        // if the square's side was adjusted, put it back
        sq.resetSide((int) origSquareSide);
    }

    private static int getNumber(String prompt) {
        String nss = JOptionPane.showInputDialog(null,prompt+"?");
        Scanner scanner = new Scanner(nss);
        return scanner.nextInt();
    }

    // REQUIRED INFRASTRUCTURE

    public Entropy(){
        paintTheImage();
    }

    public static void main(String[] args){
        SwingUtilities.invokeLater(new Runnable(){
            public void run () {
                new Entropy();
            }
        });
    }
}

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

138

139

140

141

142

143

144

145

146

147

148

149

150

151

152

153

154

155

156

157

158

159

160

161

162

163

164

165

166

167

168

169

170

171

172

173

174

175

176

177

178

179

180

181

182

183

184

185

186

187

188

189

190

191

192

193

194

195

196

197

198

199

* A program to paint an artistic representation of entropy in the NPW.

package npw;

import painter.SPainter;

import shapes.SCircle;

import shapes.SSquare;

import javax.swing.*;

import java.awt.*;

import java.util.Scanner;

public class Entropy {

private void paintTheImage(){

// determine the canvas dimensions

int canvasHeight = getNumber("Canvas height");

int canvasWidth = getNumber("Canvas width");

// set up a circle (imagining a sphere-packing problem :)

// and get the square inscribing the circle so that the lattice

// will be just perfect.

int radius = getNumber("Diamond scale");

SCircle invisibleCircle = new SCircle(radius);

SSquare sq = invisibleCircle.inscribingSquare();

// instantiate the painter and canvas

SPainter cassatt = new SPainter("Entropy", canvasWidth, canvasHeight);

// frame the canvas: we want a 10 unit frame of white on all sides.

int frameDepth = 10;

// compute the number of columns needed

// working canvas width / diameter of invisibleCircle

int totalNumberOfColumns = (int) ((canvasWidth-2*frameDepth)/invisibleCircle.diameter());

// check the work and adjust horizontal frameDepth as needed.

int horizFrameDepth = (int) ((canvasWidth - (totalNumberOfColumns * invisibleCircle.diameter())) / 2);

// compute the number of squares needed per column

int numberOfSquaresPerColumn = (int) ((canvasHeight - 2*frameDepth)/invisibleCircle.diameter());

// check the work and adjust the vertical frameDepth as needed

int vertFrameDepth = (int) ((canvasHeight - (numberOfSquaresPerColumn * invisibleCircle.diameter())) / 2);

// move the painter to the top left of the working canvas area

// remember, painter began at center of canvas

cassatt.mfd(0.5*canvasHeight-vertFrameDepth);

cassatt.mlt(0.5*canvasWidth-horizFrameDepth);

// center the painter over the first column

cassatt.mrt(invisibleCircle.radius());

// track the number of columns painted

int colNumber = 0;

// introduce a chaos factor to change things up

double chaosFactor = 0;

while (colNumber < totalNumberOfColumns){

// set the color for the column

cassatt.setColor(chooseColor());

// paint a column

paintOneColumn(cassatt,sq,numberOfSquaresPerColumn, chaosFactor);

// center the painter over the next column

cassatt.mrt(invisibleCircle.diameter());

colNumber = colNumber + 1;

chaosFactor = (1.0/totalNumberOfColumns)*colNumber;

}

private Color chooseColor() {

return Color.BLACK;

}

private void paintOneColumn(SPainter cassatt, SSquare sq, int numberOfSquaresPerColumn, double chaosFactor) {

// move down enough to paint the first square

cassatt.mbk(sq.diagonal()*0.5);

// track the amount of distance travelled

double distanceTraveled = sq.diagonal()*0.5;

// track the number of squares that get painted in the column

int squareNumber = 0;

while(squareNumber < numberOfSquaresPerColumn){

// paint a square, but as a diamond

paintOneDiamond(cassatt,sq,chaosFactor);

// move down

cassatt.mbk(sq.diagonal());

// track distance covered

distanceTraveled = distanceTraveled + sq.diagonal();

// track number of squares painted so far

squareNumber = squareNumber + 1;

}

// make sure the painter is invariant wrt position

cassatt.mfd(distanceTraveled);

}

private void paintOneDiamond(SPainter cassatt, SSquare sq, double chaosFactor) {

// set the default values

double origSquareSide = sq.side();

double rotationOffset = 0;

double offsetDirection = 0;

double offsetDistance = 0;

// when the chaosFactor is high enough, redefine the key values (sometimes)

if (chaosFactor > 0.3){

// flip the coin!

double probability = Math.random();

// for a heads, offset the diamond rotation a bit

if (probability > 0.5){

rotationOffset = (Math.random()*30)-15;

}

if(chaosFactor > 0.5){

// flip the coin!

double probability = Math.random();

// for a heads, change the size of the diamond a little bit

if (probability > 0.5){

double shrinkRate = (1 - probability)*0.7;

sq.resetSide((int) ((1-shrinkRate)*origSquareSide));

}

if (chaosFactor > 0.75){

// flip a coin!

double probability = Math.random();

if (chaosFactor > 0.9){

if (probability > 0.5){

offsetDirection = Math.random()*360;

offsetDistance = (Math.random()*(sq.diagonal()*0.5))*chaosFactor;

}

} else {

// for a heads, paint the diamond off center

if (probability > 0.5) {

offsetDirection = Math.random() * 360;

offsetDistance = (Math.random() * (sq.diagonal() * 0.5)) * 0.4;

}

// move the painter off center from the circle

cassatt.tr(offsetDirection);

cassatt.mfd(offsetDistance);

cassatt.tl(offsetDirection);

// rotate so that the square becomes a diamond

cassatt.tr(45+rotationOffset);

// paint

cassatt.paint(sq);

// rotate back!

cassatt.tl(45+rotationOffset);

// move the painter back to the center of the circle

cassatt.tr(offsetDirection);

cassatt.mbk(offsetDistance);

cassatt.tl(offsetDirection);

// if the square's side was adjusted, put it back

sq.resetSide((int) origSquareSide);

}

private static int getNumber(String prompt) {

String nss = JOptionPane.showInputDialog(null,prompt+"?");

Scanner scanner = new Scanner(nss);

return scanner.nextInt();

}

// REQUIRED INFRASTRUCTURE

public Entropy(){

paintTheImage();

}

public static void main(String[] args){

SwingUtilities.invokeLater(new Runnable(){

public void run () {

new Entropy();

}

});

}

Problem 3: Entropy in Color

Write a variant of the Entropy program which uses color, set by column. Your program might use randomized colors in some way, or it might use some range of colors to achieve some effect you like. The only constraint is that you must make some use of the chaosFactor variable in choosing your color. You should do this task as follows:

Copy the code from the Entropy class into a new class, called EntropyInColor.
Edit the EntropyInColor class, replacing all occurrences of “Entropy” with “EntropyInColor“.
Modify the chooseColor method to pick a color based at least in part on the chaosFactor. Be sure to modify the call to this method appropriately. Important: Do not remove any instructions. Do not modify any other instructions. Just modify the call to the chooseColor method, and add instructions in that method as specified.

Of course you will want to run your program a number of times to be sure it’s doing what it’s supposed to.

Problem 4: Hirst Lattice

Write a variant of your EntropyInColor class in your npw package which paints images like the one shown. Call this program HirstLattice. Moreover, do this task by:

Copying and pasting the code from the EntropyInColor file to a newly established HirstLattice file.
Edit the HirstLattice file by replacing all occurrences of “EntropyInColor” by “HirstLattice” and also modifying the leading comment.
Replace the chooseColor method with the randomColor method we’ve seen in lab, and modify your program so that it chooses a random color for each diamond it paints. Moreover, remove the code which causes random variation in diamond size, rotation, and position.

Run your program a number of times to see that it is doing what it is supposed to do.

Problem 5: Hirst Dots

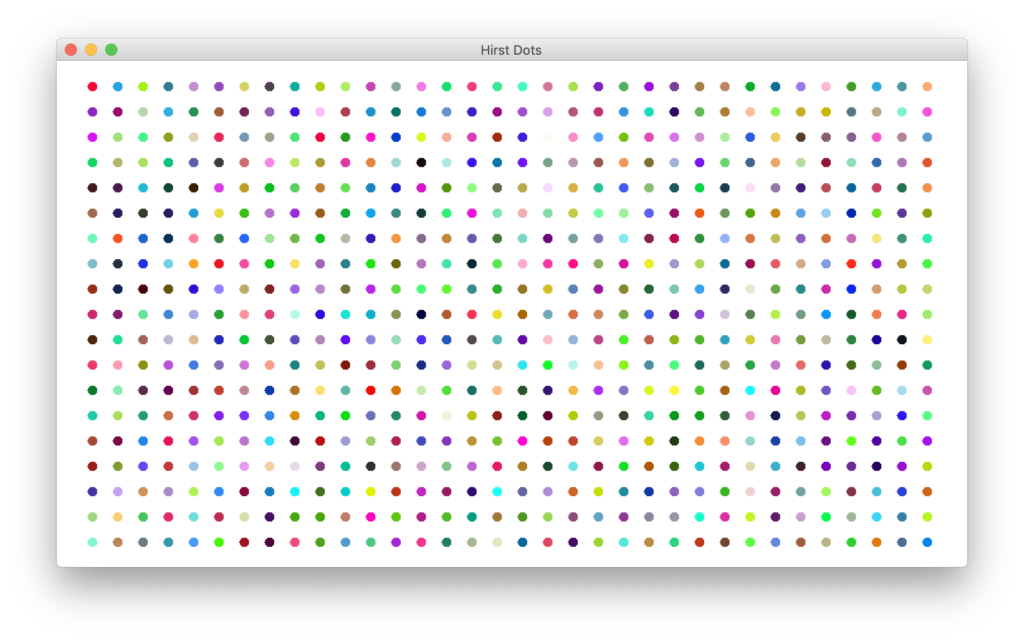
This one requires a couple clever thoughts! Be sure you have read and understand all of the code in the previous two problems.

Write a variant of your HirstLattice class in your npw package which paints images like the one shown. Call this program HirstDots. Moreover, do this task by:

Copying and pasting the code from the HirstLattice file to a newly established HirstDots file.
Edit the HirstDots file by replacing all occurrences of “HirstLattice” by “HirstDots” and also modifying the leading comment.
Do what needs to be done to your program to paint circles instead of diamonds. Moreover, paint the circles at half the size of the diamonds we painted before.

Run your program a number of times to see that it is doing what it is supposed to do.

Problem 6: Deterministic Invention

Write a program called Invention1 in your npw package which paints an image subject to the following constraints. Do not just modify the above programs in 2-5 – make your own thing! Your invention should be significantly different from other students’ inventions!

It uses at least one while statement in a nontrivial way.
It uses at least one if statement in a nontrivial way.
It features both circles and squares, all created from just one SCircle and just one SSquare. No SRectangles.
It creates the exact same image every time it is run.
There is some chance that the casual observer might find the image interesting!

Run it (at least) twice to make sure the output is the same each time you run the program.

Problem 7: Nondeterministic Invention

Write a program called Invention2 in your npw package which paints an image subject to the following constraints. Do not just modify the above programs in 2-5 – make your own thing! Your invention should be significantly different from other students’ inventions!

It uses at least one while statement in a nontrivial way.
It uses at least one if statement in a nontrivial way.
It features solely rectangles, all generated from a single SRectangle.
The program takes no input from the user of the program.
It creates a different image each time the program is executed, different with respect to number or size or color or whatever of the featured object.
There is some chance that the casual observer might find the image interesting!

Run it twice to make sure the output is not the same each time you run the program.

Problem 8: Pinwheel

Write a program called Pinwheel in your npw package which paints images like the ones just presented. The constraints are these:

The number of squares will be read from a dialog box.
Two randomly chosen colors will be used for the image that is painted when the program is run.
The canvas will be of size 600 by 600 and the square will be 400 by 400.

Run the program several times, doing your best to enjoy looking at the output.

The Exit

Due date: Tuesday October 31, 2023.
Once you are ready, you must demo your programs for one of the TAs.
You must post your work, a source program and an appropriate demo for each problem (Standard Output Stream for the first problem, images for the remainder of the problems), to your Web Work Site before you demo in order to receive credit.

Hi There!

Programming Challenge 4: Nonrepresentational Artistic Expressions

Overview

Why do it?

The Entrance

Problem 1: The Cave

Problem 2: Entropy

Problem 3: Entropy in Color

Problem 4: Hirst Lattice

Problem 5: Hirst Dots

Problem 6: Deterministic Invention

Problem 7: Nondeterministic Invention

Problem 8: Pinwheel

The Exit