Overview
Your task is to write four separate Java programs for this assignment, all in the context of the NPW. Special notes for these programs:
- All of the programs will make use of the shapes functionality of the NPW world, but not the painter functionality.
- Unlike most programs that you will write this semester, you are required to place all of your executable code for each program in this assignment within just one method – the main method. (There will be no infrastructure for painting in these programs, hence no paintTheImage or similar method.) This is not only because the solutions to the given problems will be relatively short, but also because we will want to reflect more upon the creation and use of objects in these programs than on the structure of the programs.
- The use of arithmetic operators to directly compute areas or perimeters of shapes, diagonals of squares or rectangles, diameters of circles, is strictly prohibited. Thus, you must create and use shapes in order to compute such values.
- It is required that you name each number that you use in the program, other that small integers whose meanings will be readily apparent to even the most casual of readers.
Why do it?
By completing this computational problem solving assignment you will:
- Demonstrate the ability to make use of the problem solving strategy of problem decomposition.
- Demonstrate the ability to make use of the problem solving strategy of imaginative construction.
- Gain considerable practice in the creation and use of “objects to think with”.
- Gain significant experience with infrastructural elements of the language, with types and variables and expressions, in particular.
The Entrance
Lab 4 should be viewed as an important element of preparation for this assignment, so you want to be sure to have completed that lab prior to starting this assignment. You should also study the functionality associated with simple shapes in Appendix 1 of your Laboratory Manual.
Problem 1: The Messy Table
Consider a messy circular dining room table after a late night of studying for a CSC212 exam, covered in plates, cans, a lab manual, and some notebooks. The oak table measures 40in in diameter. On top of the table sit two notebooks, each of size 8.5x11in, and a lab manual of size 10.5x14in There are also three square white coasters upon which sit empty Mountain Dew cans. The cans have a radius of 1.25in and perfectly inscribe the coasters. Finally there are four smallish 7in diameter plates which previously held snacks of quesadillas (since it was recently National Quesadilla Day) spread around the table. None of the objects on the table lie atop any others (except for the cans upon the coasters).
Write a program called WorkSpace in a package called shapes to display the area of the table which is not obscured by any object and may still be used for studying. In doing so, you are required to write your program in a manner that is more or less consistent with the following guidelines:
- Introduce a variable for each of the given measurements, and bind these variables to the measurements. Be sure to choose meaningful variable names. And be sure to refer to the values by means of the variables in the rest of your program.
- Create six “objects to think with” from the NPW, one for the table, one for a book, one for the lab manual, one for a plate, one for a can, and one for a coaster. Of course, you don’t merely want to create them, you want to introduce variables for each, and appropriately bind the variables to the objects. Constraint: Do not use an explicit constructor to construct the coaster. Rather, informally speaking, ask the can to produce the coaster.
- Introduce a variable and bind it to the collective area of the objects on the table.
- Introduce a variable and bind it to the result – the area of the table not obscured by the objects which sit on top of it.
- Display the result to the standard output stream, being sure to give it a label.
Problem 2: The 8-Sided Die
An 8-sided die has 8 equilateral triangles (those where all edges have the same length) making up the faces. One edge of such a die is 16mm long, and each pip (dot) on a side is a circle of diameter 3mm. On an 8-sided die, the number of pips range from 1 to 8 on each side. See the below image for a bit more of an idea of how this looks.
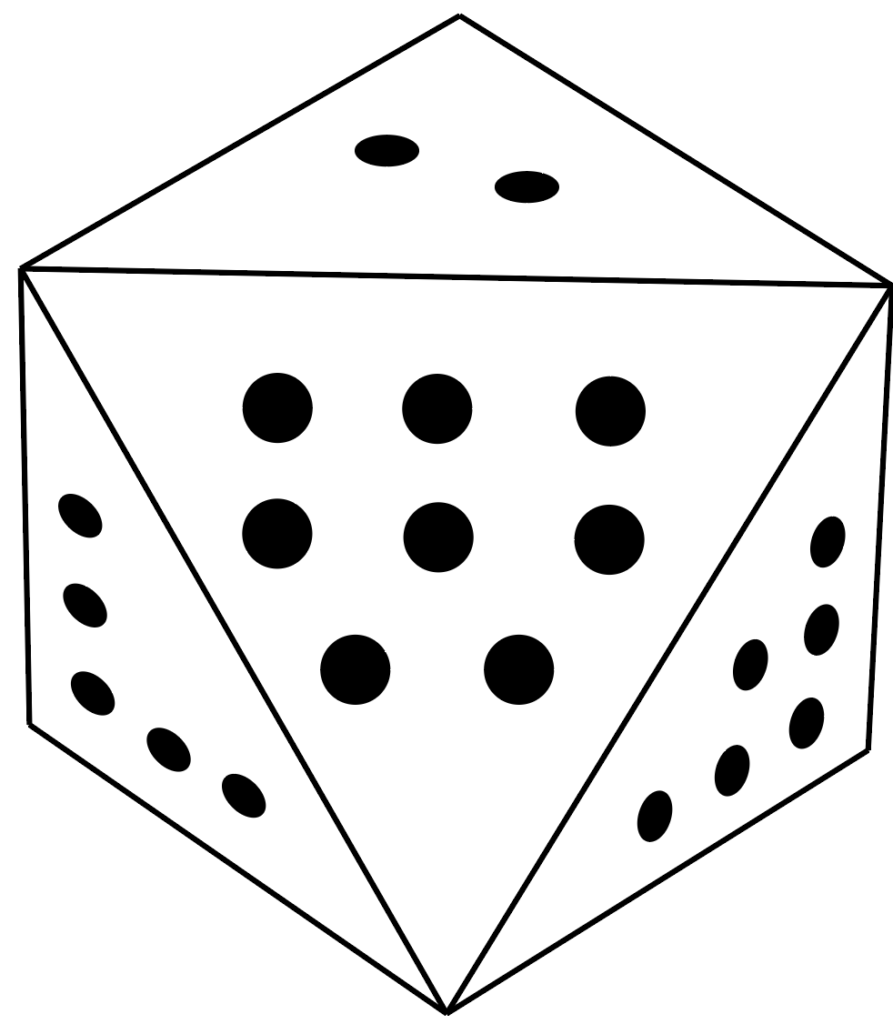
Write a Java program called D8WhiteSpace in the shapes package which computes the total area on the die not covered by one of the pips. In doing so:
- Name the values that serve to define the particular problem instance (those related to die size and pip size in this case).
- Model objects that can be used to solve the problem in a fairly natural way. In order to do this you should read through the appendix for NPW and recognize that we have a way to think with regular polygons. Those are shapes with a certain dimension (number of sides) wherein all of the sides are the same length! Perhaps you’ll want to experiment with this functionality a bit before attempting this problem.
- Strive to present a simple expression of a solution which is grounded in sound problem solving strategies (problem decomposition, in this case).
- Clearly, meaningfully, label the program output.
Problem 3: Colorful Tapestry
Write a Java program called ColorfulTapestry in the shapes package to compute the area of the purple space in the below image of a tapestry.
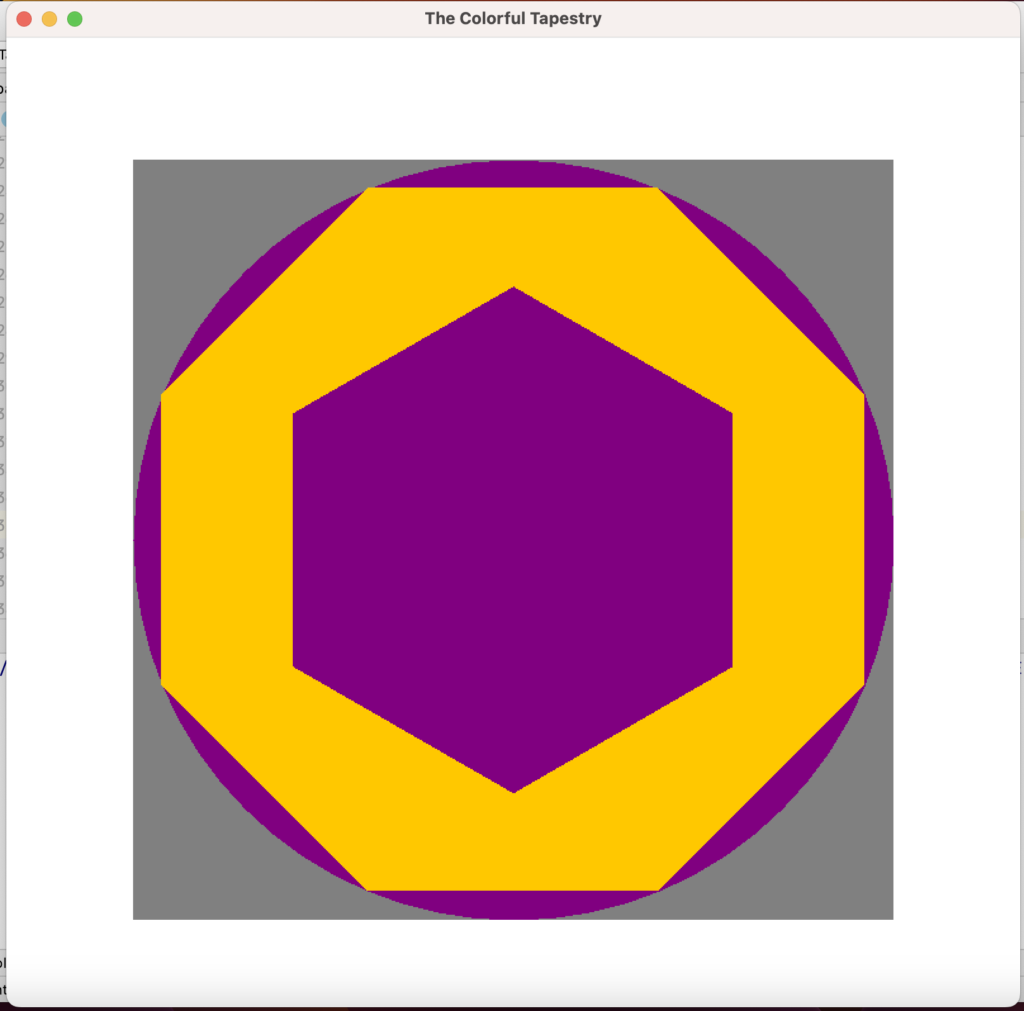
The side length of the tapestry (grey square) is 600mm. The points at the top and bottom of the purple hexagon are exactly 100mm from the midpoints of the sides of the grey square.
In writing this program, you are required to proceed in a manner that is more or less consistent with the following guidelines:
- Name the values that serve to define the particular problem instance (edge length and distances from corner/circle to midpoint in this case).
- Make use of the problem solving strategy of imaginative construction by mentally overlaying some number of shapes on the image that can be exploited in the service of solving this problem. In fact, you should really draw them on the image provided.
- Model objects that can be used to solve the problem in a fairly natural way – the tapestry, the purple circle, the orange octagon, and the interior purple hexagon. In doing so, bring to bear computational manifestations of your imaginative constructions.
- Strive to present a simple expression of the solution which is grounded in the problem solving strategy of problem decomposition.
- Clearly, meaningfully, label the program output.
Problem 4: The Pool Shot
Consider a standard pool table, which has a playing area of 88″ by 44″. A pool table has six pockets, one in each corner and one in the center of each of the long edges. If we consider one of the long edges to be the ‘top’ of the playing area, then we can number the pockets clockwise from top-left 1 through 6. Let’s also create coordinates on our table starting from the top left. For example, pocket 1 lives at (0,0), pocket 3 at (88,0), and pocket 4 at (88,44).
If a ball is placed on the table at coordinate (x,y), and is struck so that it hits the top of the play area at position (k, 0), we would like to know whether the ball goes in to pocket 4. In a new Java class called PoolShot inside the shapes package, use a prompt and a scanner to ask the user for x, y, and k. Do your work roughly as follows:
- Create a nice drawing of the pool table.
- Add a ball to your table and draw a line from the ball to the top of the play area. Draw another line at the same angle, but mirrored vertically from the point where the ball hit the top of the play area. (Note that if this line hits pocket 4, then the ball would go in.)
- Introduce a variable for each of the values of interest, binding them to values read from the user using a Scanner reading from the standard input stream.
- Introduce a rectangle to help capture the diagonal nature of the line from the ball to the top of the play area.
- Using a little physics, you can prove to yourself that the line from the top wall to the pocket is a scaled up version of the line from the ball to the top wall. You can compute how much you need to scale up by dividing the height of the table by the y-coordinate of the ball.
- Create a variable called key, and bind it to a rectangle which has been scaled up the appropriate amount so that its diagonal captures the line leaving the top of the play area. This rectangle has the right height (that of the pool table), but possibly not the right width to get from point (k,0) to the pocket.
- Display, nicely labeled, the final x-coordinate of the ball. This coordinate is not the width of the key – you need to do more work than that! Note that this coordinate may be outside the bounds of the table, since we aren’t checking that yet.
- Write a selection statement to determine if the final x-coordinate is between 87 and 89. You may need to nest an if-statement inside another if-statement. If the final x-coordinate is between these values, output that the ball enters pocket 4. Otherwise, output that it does not.
Due Date and Reminders
- Due date: Tuesday, October 17, 2023
- Once you are ready, you must demo your programs for one of the TAs.
- You must post your work, a source program and a standard output stream demo for each problem, to your Web Work Site. You may not demo until your work is posted on your Web Site!