Overview
Your task is to write computational solutions to three problems, two in the context of the Nonrepresentational Painting World (NPW), and one in the context of the Modular Melody World (MMW). This is meant as a followup to, or second part of, challenge 1. As before, relatively rigid constraints will be placed on you as you engage in these tasks, as is appropriate early in a CS1 course.
Why do it?
By composing Java solutions to the problems in the context of the featured microworlds you will:
- Gain considerable practice in creating and using objects.
- Continue to get acquainted with elements of graphics programming and sonic programming.
- Program, at least some of the time, in a manner that is consistent with the principle of stepwise refinement.
- Make explicit use of the problem solving strategy of problem decomposition.
- Write programs with invariance in mind.
- Learn just a bit about how to work from language specifications.
- Explore the notion creativity from constraint in the course of microworld problem solving.
The Entrance
Please be sure to complete Lab 2 and Programming Challenge 1 before starting this assignment.
Problem 1: Geometric Art
In the context of the NPW, write a program called GeometricArt within the npw package to paint an image much like the one depicted below.
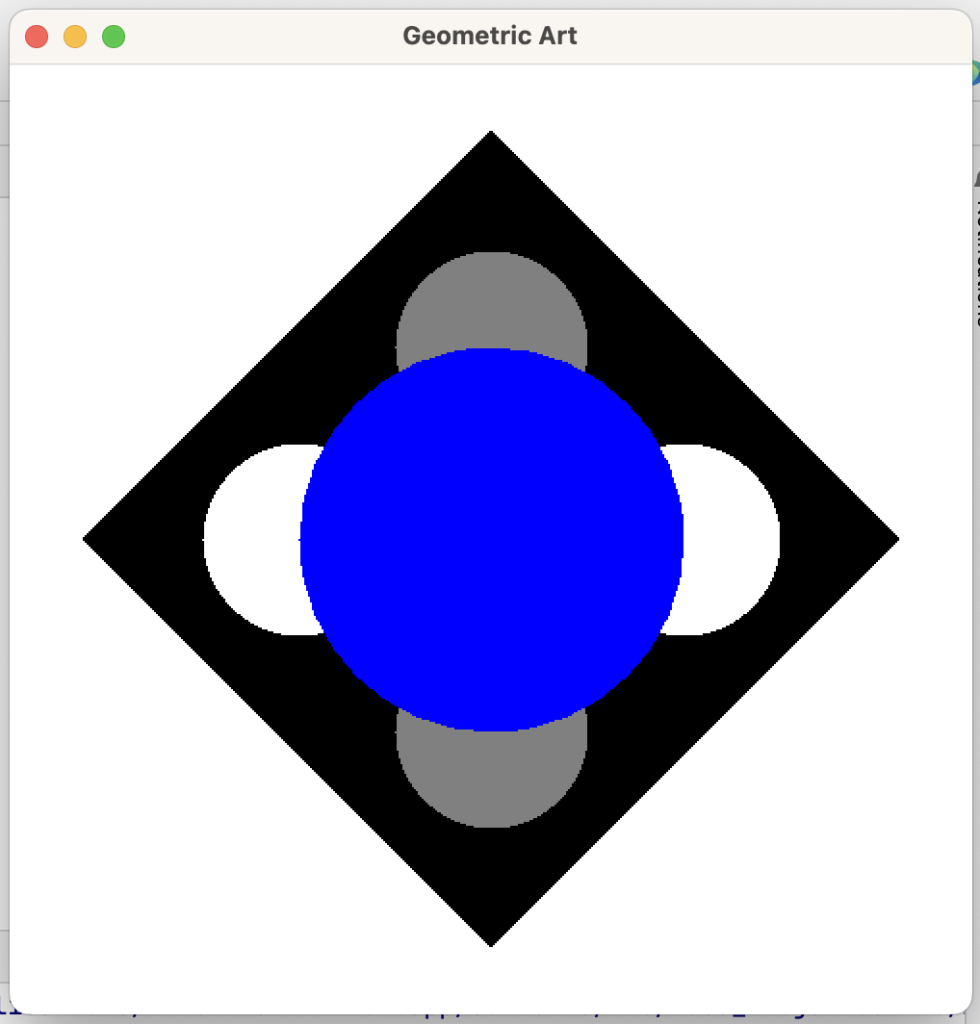
Constraints:
- Use the technique of modifying an existing program that does something similar. Do so by:
(a) Creating a new Java Main Class file for the program, naming it GeometricArt and placing it in the npw package.
(b) Replacing the entire contents of the GeometricArt file with the entire contents of the BlueDot program.
(c) Changing all occurrences of BlueDot to GeometricArt. - Place the following code, without alteration, in the paintTheImage method.
Then:123456789SPainter cassatt = new SPainter("Geometric Art", 500, 500);SCircle dot = new SCircle(100);SSquare box = new SSquare(300);paintBlackSquare(cassatt,box);paintGrayCircles(cassatt,dot);paintWhiteCircles(cassatt,dot);paintBlueCircle(cassatt,dot);
(a) Use the features of IntelliJ to add the necessary import statements.
(b) Use the light bulbs to create a stub for each of the unrefined methods. (You should create 4 stubs.) - One at a time, complete the definitions of the methods, proceeding as follows:
(a) Run the program, and see that not much happens.
(b) Refine the paintBlackSquare method, being sure to make it invariant with respect to both the location and heading of the painter, run the program, enjoy the black square. Note that you’ll need to set the heading of the painter to 45 degrees to paint this square.
(c) Refine the paintGrayCircles method, being sure to make it invariant with respect to both the location and heading of the painter, run the program, enjoy the black square and gray circles.
(d) Refine the paintWhiteCircles method, being sure to make it invariant with respect to both the location and heading of the painter, run the program, enjoy the black, gray circles and white circles.
(e) Refine the paintBlueCircle method, run the program, and enjoy looking at the geometric art!
Problem 2: Dots
In the context of the NPW, write a program called Dots within the npw package to paint an image consisting exclusively of painted and drawn circles subject to the following constraints:
- the program creates and uses only one SCircle object
- it contains exactly 7 drawn (not filled in) circles
- it contains at least 2 painted (filled in) circles
- it contains circles of exactly 3 different sizes
- it contains circles of exactly 4 different colors
- none of the drawn circles touch (but the painted ones can touch!)
- the image is symmetric about the Y-axis, including with respect to color (i.e., the left and right sides of the image are a mirror image of each other)
- not all of the drawn circles touch the Y-axis
Problem 3: Take a Walk!
Write a program called WalkingMelody within the mmw package to play a melody composed exclusively of the melodic sequences available in MMW which are motion themed (the ones from Problem 3 of Challenge 1), subject to the following additional constraints:
- The melody will consist of between 43 and 45 notes.
- The melody will make use of exactly 5 different modular melodic sequences (all drawn from the motion/locomotion modular melodic sequences). You may need to use one or more of these 5 more than once!
- At least one of your melodic sequences must be named after walking – i.e., you have to use a melodic sequence with Stroll in its title.
- You must ask the composer to raise its note at least once.
- The melody must be invariant with respect to pitch.
Be sure your program enables the textual output for the composer so that you can demo it to TAs in the lab (where only a few computers have speakers).
Due Date and Reminders
- Due date: Tuesday October 3, 2023
- Once you are ready, you must demo your programs for one of the TAs.
- You must post your work (source program and demo for each problem), to your Web Work Site. You can not demo until your work is posted on your Web Site!