The Department of Computer Science & Engineering
|
|
CSE 111: Great Ideas in Computer Science
|
Alan Turing is often called "The Father of Computer Science." He has contributed major insights to the fields of theoretical computer science and artificial intelligence, not to mention his important work during WWII in breaking the German enigma code.
We'll talk about his influence in AI later in the course, but todays lecture is based on some of his contributions to theoretical computer science.
Unfortunately Turing did not live very long - only until age 41. Unlike many other paradigm shifting scientists of old whose ideas prompted their persecution, Turing's sexuality was unfortunately his undoing. In the eyes of the British courts in 1952 he was a pervert for being a homosexual (as it was illegal in Britain until 1967). When he was found guilty his security clearance was revoked and he was forced to stop his cryptoanalysis work for the government. He died of cyanide poisoning in 1954, believed to be suicide.
For more information:The Turing Machine
A Turing Machine is a conceptual model of a computer. It is able to do everything the computers we use every day are able to do, but the model is meant to be simpler. Instead of having to talk about a specific architecture of a computer (whether it be our calculator, or desktop computer, or something else) we can just talk about this single simple model. It is used often by theorists in proving things about what problems are computable. It is widely believed that for every algorithm there exists a Turing Machine which computes it.
The formalization of a Turing Machine we will use is:
Rapaport, William J. (1985), "Turing Machines" [PDF], from Morton L. Schagrin, Randall R. Dipert, & William J. Rapaport, Logic: A Computer Approach (New York: McGraw-Hill, 1985): 327-339.
I will describe it in part here, but you should read the above paper for the full treatment. Some of the diagrams in this section are from that text.
Turing Machines (TMs) have a lot in common with the Finite Automatas we've already discussed. A TM has a finite control unit which works much like a FA, changing states based on what the tape is reading. The state register keeps track of what the state currently is. The big difference from an FA is that the machine reads and writes to a (at least conceptually) infinite tape. What we mean by this is that we can always add to the tape - we never run out. We can check whether we are at the beginning or end though of the tape that exists, and cut off a piece from the end. We can change values and add things to the tape as well. The TM therefore has memory and can perform tasks producing output, which an FA cannot do.
The main limitation to this is that the TM can look at only one "square" on the tape at once. Each square of the tape contains either a 1 or 0 when we begin (this is the input to the machine), and with this and the pre-programmed algorithm we have to produce output on that same tape.
Our TM is thought of as a machine on wheels, with a paper tape stretched across the top of the machine. The machine has a scanner which looks at one square of the tape at a time. It's able to read a 1 or 0 from the tape, and also write a 1 or 0. Inside our TM is some programming which tells it what to do when it sees a 1 or 0. Upon each input it switches states (which we can think of as a mental state of mind in a human). It also has a state register, which just tracks which state the machine is currently in.
The programs (algorithm) the TM is capable of executing are also quite limited. They contain only 5 kinds of instructions:
Very crucially these instructions are enough to do the sequence, selection, and loop we have talked abut in class. Even more importantly though, it was shown in the Church-Turing thesis that EVERYTHING that can be computed, can be computed using a Turing Machine!
We can draw a program for the TM using a flowchart (similar to the decision trees we've discussed previously).
The flow chart contains 3 types of blocks:
We'll also add two more decision blocks to test whether we are at the LEFTEND or RIGHTEND of our tape. Since our tape is assumed to be as long as we need it to be, moving past the end adds another square to our tape. If we need to remove a square from the tape, we use ERASE.
That specifies the machine. That's really it - with this we now have the ability to do computation!
Also, there are many TM simulators on the internet. This one seems particularly good, and I recommend using it (or one like it) when writing your own Turing machine code to test it.
Some Turing Machine Programs
Let's start with a machine which negates some binary input. That is, if the input is 110, the machine's tape would contain 001 after the program has executed.
Lets start by defining a program for our machine to execute.
The state M0 handles actually changing the value of the square we're currently looking at. The state M1 determines if we are done yet. If we aren't, we go back to M0. These programs are much easier to see and understand when in flowchart form:
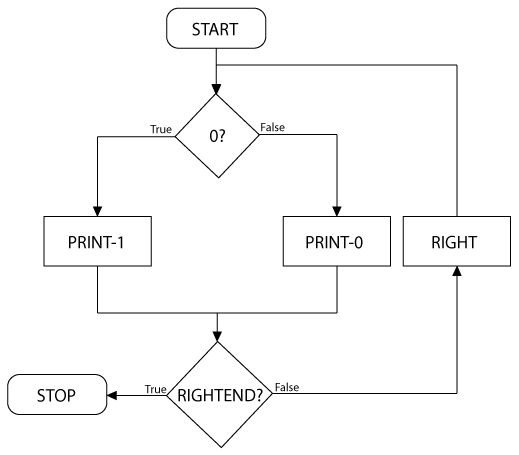
In-Class Exercise: Create a TM which on its tape when it starts is only a single symbol (1 or 0). Make your machine write the negation of the single symbol in the square to its right. It's probably easier to draw the flow chart before the program.
Our next TM will be one which determines the truth value of two binary digits after taking the disjunction (OR) of them.
The idea is that M0 checks the first square. If it's a 1 we already know our OR will succeed, we move right and go to M2 which just moves right again and puts us in M3 (which prints the 1 and ends the program). If M0 was a 0, we depend on the value of the second square. So we move right and are in state M1. If M1 is a 1, the answer is true and we switch to M3 again. If it is a 0, the OR is false, so we go to M4 which prints a 0 and stops.
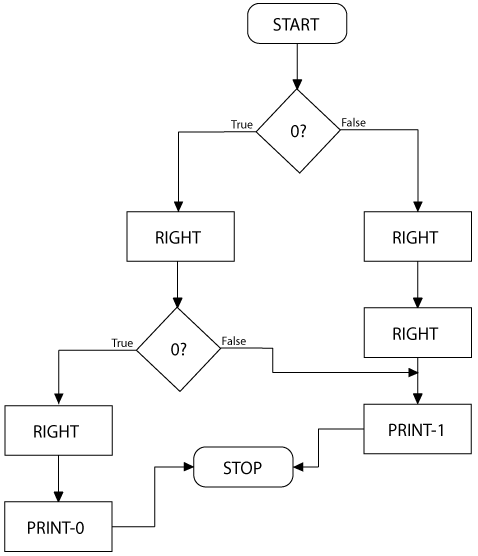
In-Class Exercise: Create a TM and flowchart for the conjunction (AND) of two binary digits. Write the result as a single digit after the input, as we did above.
The Universal Turing Machine
It may seem crazy, but people have actually built Turing Machines! Take a look at these: