How Computers Work: Binary Arithmetic and Boolean Algebra

Named after the Hungarian-American mathemetician John von Neumann, the von Neumann architecture is an abstract design of modern computing systems which have a central processing unit and separate storage (memory) to hold programs and data. It is equivalent to the Universal Turing Machine (which we will discuss in a few weeks). Unlike the Universal Turing Machine though, this architecture is closely related to the functional description of todays computer systems. It is made up of four parts - memory, a control unit, an arithmetic logic unit (ALU) and input/output (I/O).

• Memory: A location in which to store both instructions (the 'program') and data to be used by the program. The instructions are modifiable by the instructions themselves in the same way as data, leading to the ablity to have programs which can write or modify their own instructions.
• Control Unit: Executes instructions stored in memory. It contains a "Control Counter" which tracks what instruction is currently being executed and can be changed by the instruction.
• Arithmetic Logic Unit: The ALU is the primary component of what we call the CPU or Central Processing Unit of a computer. It performs some logic and arithmetic operations.
• Input/Output: Input and output are written to and read from an accumulator which stores input or output for a program being run.

The numbers we're used to are in what we call base 10. That is, we have 10 digits, 0 through 9. Moreover, when we look at a number we're used to, say

4735

We say 5 is in the ones spot, 3 is in the tens spot, 7 is in the hundreds spot, and 4 is in the thousands spot. This is because we could represent this number as:

4000 + 700 + 30 + 5

Or, equivalentely, as

4*10³ + 7*10² + 3*10¹ + 5*10⁰

Binary numbers use all the same concepts, except they are in base 2, that is, the only numbers available are 0 and 1.

So, lets consider the binary number 1110. Using our above technique, and changing the 10 to a 2, we can do the following:

1110 = 1*2³ + 1*2² + 1*2¹ + 0*2⁰ = 8 + 4 + 2 + 0 = 14

So, you see, each position is a power of two... binary numbers have a ones, twos, fours, eights, etc... position. What we did above is all you ever have to do to convert a binary number to decimal. But what about decimal to binary?

Well. it's a little trickier, but only because you have to know your powers of two. You'll definitely want to memorize them up to some suitably large number like 1024.

Lets consider the number 123. The first thing we do, is look for the largest power of two which can be subtracted from it. In this case, it is 64.

Subtract 64 from 123 to get 59. We write a 1 in the 64's spot of our binary digit. Any spots we don't set to 1, are by default 0. We continue this process, as below:

-	123
1	59
11	27
111	11
1111	3
111101	1
1111011	0

Therefore, when we're done, we see our binary number is 1111011. We can follow the above technique for converting back to decimal to check ourselves:

1111011 = 1*2⁶ + 1*2⁵ + 1*2⁴ + 1*2³ + 0*2² + 1*2¹ + 1*2⁰ = 64 + 32 + 16 + 8 + 0 + 2 + 1 = 123

There is an alternative approach to converting decimal to binary that you may find easier - the division method. Consider again our number 123. Since it's less than 128, we know there will be 7 bits in the result, so lets create a table with 7 slots:

Okay, now, we divide 123 by 2 and put the remainder in the far right slot. 123/2 is 61 with a remainder of 1, so we have:

						1

Next we divide 61 by 2 and get 30r1, so we put a 1 in the next slot:

					1	1

30/2 is 15r0, so the next slot is 0:

				0	1	1

We continue this process until we are at 0, giving us:

1	1	1	1	0	1	1

Which is our expected answer!

We can use this same technique for converting to and from ANY number system! Let's practice with the number AE5 in hex, that is, base 16 (in base 16 A = 10, B = 11, C = 12, D = 13, E = 14, and F = 15). The answer is 2789, but can you get it yourself? What about convert it back?

Check out this page for a worked example including base 2, 8, and 16.

I'm sure you've all heard of bits, bytes, kilobytes, and so on... But do you know what they mean?

1 bit is a single 1 or 0.
1 nibble is 4 bits (we don't really use this, its just interesting).
1 byte is 8 bits.
1 kilobyte is 1024 bytes.
1 megabyte is 1024 kilobytes (KB).
1 gigabyte is 1024 megabytes (MB).

and so on, through terabytes, petabytes and exabytes.

Why is a byte 8 bits though? That seems rather arbitrary! Well, the first computers worked with numbers with a maximum size of 8 bits (up to 255 in decimal - that's 2⁸-1). Todays computers are mostly 64-bit, meaning they work with numbers up to 64 bits in length (2^64-1 = 18446744073709551615, wow!)

We've seen how to represent numbers in a computer, but that's really not terribly interesting. How do we represent text? graphics?

Text turns out to be not all that interesting actually. We simply have assigned numbers to letters. This was first done in 1963 with the ASCII standard. This really shouldn't be surprising - Samuel Morse represented text as dots and dashes (effectively ones and zeroes) in the mid-1800s.

Okay, so let's turn our attention to images, and first black and white ones. We save images as bitmaps. Which is a map, made of bits (as you might expect!)

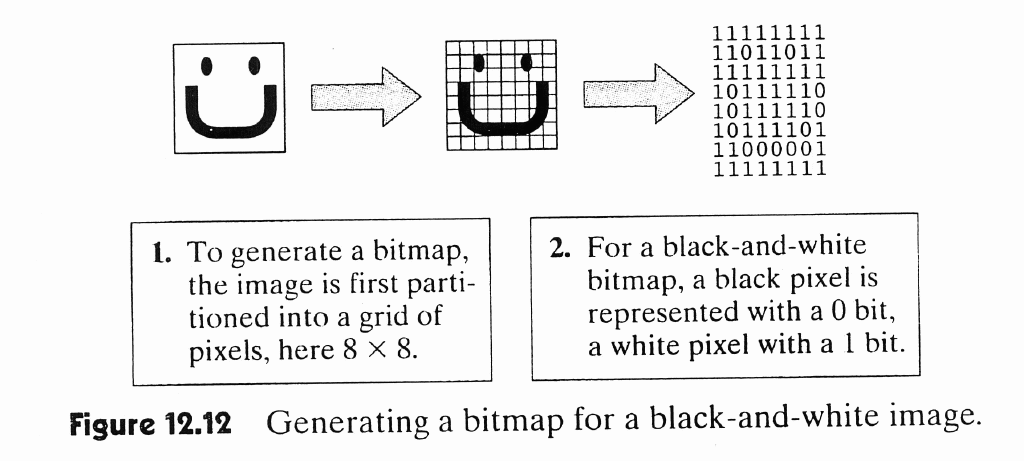
A color can be represented using three numbers representing their red, green, and blue content - we call this RGB color coding. Each of these numbers range from 0-255, so, for example, (0,0,0) is white, (255,0,0) is Red, and (125,0,0) is pink.

An RGB table

So, for color images, these three numbers are converted to binary for each pixel and stored.

In-Class Exercise: How can we represent an audio clip in binary?

We've shown how we can represent things using binary numbers, but now we should show how we can manipulate them. This is known as Boolean Algebra and was discovered by George Boole and published in his book An Investigation of the Laws of Thought in 1854. This later became the basis of how computers function.

It turns out that all of the operations we can do with binary numbers come from logical operations: AND, OR, NOT, and XOR.

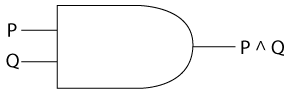
AND: The result of taking the conjunction of two binary inputs is 1, only if both of the inputs are 1.

P	Q	P^Q
0	0	0
0	1	0
1	0	0
1	1	1

We can draw this as what we call an "And Gate" for use in circuit diagrams (we'll do a little with this later).

OR: The disjunction if two inputs is 1 if any one of the inputs is 1 (true).

P	Q	P v Q
0	0	0
0	1	1
1	0	1
1	1	1

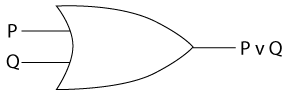
NOT: The negation gives the opposite truth value of the input.

P	~P
0	1
1	0

XOR: Exclusive-Or is a disjunction which is not true when both inputs are true.

P	Q	P (+) Q
0	0	0
0	1	1
1	0	1
1	1	0

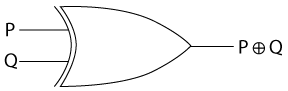
Let's look at something a little more complex where we can compose these with each other: (~P v Q) ^ R

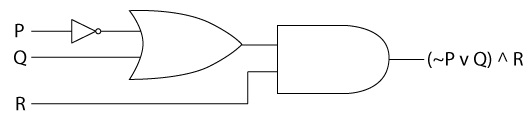
P	Q	R	~P	~P v Q	(~P v Q) ^ R
0	0	0	1	1	0
0	0	1	1	1	1
0	1	0	1	1	0
0	1	1	1	1	1
1	0	0	0	0	0
1	0	1	0	0	0
1	1	0	0	1	0
1	1	1	0	1	1

In-Class Exercise: Draw the circuit and truth table for (~A ^ B) v (A ^ ~C)

Note that I said that the computer was made up of transistors, and these logic gates don't seem directly related! It turns out they are though, see this page for some examples if you're interested! There is a lot more we could say about circuits and boolean algebra. If you are interested in these things, I recommend the website All About Circuits as a place to learn more, and specifically this chapter.

Adding binary numbers is easy, here's all you need to know:

0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0 (with a carry of 1)

And really that's it! The technique we use is exactly the same as the one you're used to from elementary school. Lets look at an example:

Just as with decimal arithmetic, we can take extra spaces to the left as "0" ... Consider the following:

This works fine for positive numbers, but when we deal with subtraction we're really dealing with adding a negative number and we don't yet have a way to represent that! In order to solve this, we use an alternate technique known as "Two's Compliment."

We know that a single byte (ie. 8 binary digits) can represent from 0 to 255. The idea behind two's compliment is to make the most significant bit (in this case the 128-place) represent the sign (0 for +, 1 for -) and invert some of the numbers (in a way we'll show) to make math work out naturally. In 8 bits, we'll now be able to represent -128 to 127.

First I'll give an algorithm that explains how we convert a number to its two's compliment, then I'll show why we do it this way.

1. Express the binary value for the positive number (ie. the absolute value of the number)
2. If the original number was negative:
   1. Compliment the value (flip all of the bits 0 to 1 and 1 to 0)
   2. Add 1
3. If the value is positive, add zeroes to the front of the number to have the proper number of bits.
4. If the value is negative, add ones to the front of the number to have the proper number of bits.

Okay, let's consider the number -13, and say we want the 8-bit 2's compliment of it (ie. we want the length to be 8 bits). First we represent the absolute value of -13 (written |-13|, which is 13) in binary:

13₂ = 1101

Since it was negative, we flip all of its bits:
1101 -> 0010
Then add 1:
0011
Now, it's negative, and we want 8 bits, so we pad with 1's to the left:
11110011

And that's our 2's compliment! But still, how does this help us? Well lets say we want to add 14 to this. We expect the answer to be 1.

We also end up with a carry of 1, which we just ignore (we're limiting ourselves to a maximum number of bits, so this is expected!) And look - our answer is 1, just as we expected! So, we get negative numbers by doing a little extra work up front, but we get to use the same adding technique we already learned.

Note: Decimal numbers are way harder. The real numbers are extremely infinate. We all know there's an infinite number of integers. Well there's an infinite number of reals between 0 and 1 even. In fact, there's an infinite number between 0.000001 and 0.000002 or any other arbitrarily small difference in numbers. Therefore any way we represent these numbers is going to involve approximations (which makes sense - how would you represent Pi in a computer without an approximation?)

A and B represent two binary inputs, S is the sum, and C is the carry. This is very limited, but chaining these together gives us the ability to add numbers of any size.

Let's look at the truth table for it:

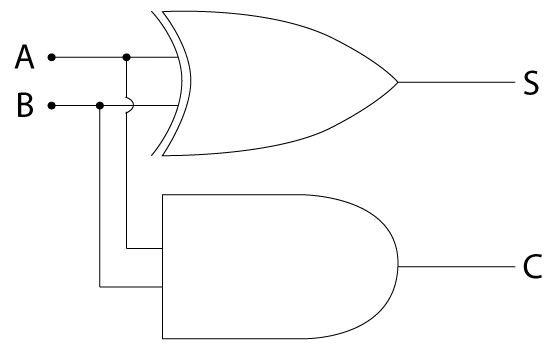
A	B	S	C
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

It's exactly the same as the chart shown earlier where we showed what should happen when two bits are summed!

Right! Good point! But, this really ends up just being another representation problem. I'm afraid we won't see the complete solution until we talk about Turing Machines though!