Lab 3 - Keeping Secrets Safe

Data encryption is how we keep our information safe on the internet whenever we are asked for our credit card number, or a password to a website. There are several different kinds of encryption algorithms - some of which are much more sophisticated than others.

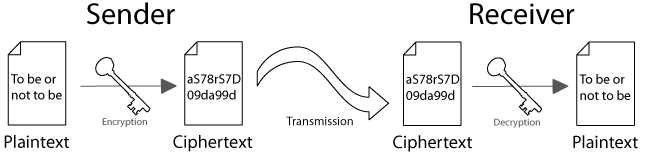
The basic idea is that plain text is converted by the sender of the message using some encryption algorithm to coded text (called ciphertext). The ciphertext is then transmitted across an unsafe medium (whether it be the internet, or just passing the message through a room of people where anyone could see it). On the receiving end, the receiver applies some decryption algorithm to recover the original text.

Shared codebook:

In this technique, both parties must already know some sort of code translation algorithm in advance in order to share data. A shared code book can translate letters, sequences of letters, bits, or bytes, or other sequences for others. There can be complex schemes used in the translation (for the first three letters, use this rule. For the next use this other rule. etc...). A code book contains only a list of decoding options. Somehow the receiver must know which of the options to use for the data received.

There are many problems with this technique though - somehow both you and your friend need to get the code book and the scheme for decoding. If someone who was previously your friend is no longer, you must change the code for everyone since there's no way to revoke access to a code. You'd need a lot of these to have unique codes for each person you corresponded with. This was the problem the Germans ran in to in WWI, when a codebook was seized early in the war and used to decrypt important documents such as the Zimmermann Telegram.

The most simple codebooks can be made by writing a series of 26 unique symbols and letters down the edge of a page. A key is decided upon and that symbol in the code is taken to be A, the next is B, and so on, looping back to the beginning of the list when you reach the end.

This is known as a substitution cypher since all you are doing is substituting one letter for another. This turns out to be very easy to crack by using knowledge about the language and letter frequencies. For example, in English if a word is a single letter it is going to be either an 'a' or 'i'. Also, the letter 'e' is the most common letter in English - representing 12.7% of all the letters we use.

The German enigma machine was just a substitution cypher as well, but what made it difficult to crack were two special properties: the messages were first codified so that words or pairs of words were replaced with pairs of letters from a codebook, and as the user entered the text into the machine there were cogs which would rotate changing the cypher being used. Therefore every letter was coded using a different cypher! Which cyphers were used was handled by a series of wires hooked up to the machine in a pre-defined (and rotating) manner. This code was cracked though, as we have already learned.

One-way functions:

We have learned in class that text can be easily represent as numbers. It is natural to perform mathematical operations on a number, and many mathematical operations are easily reversed.

A one-way function is a function which is easy to calculate, but it's inverse is very difficult to calculate. This is much different from a normal function. Consider for example y = x + 3. The inverse of this function is found by solving for x: x = y - 3. Solving for x was easy, and now we have a way to reverse the original function. We want a function that is really hard to find the inverse of. [Aside: We generally mean that the encryption algorithm and an algorithm to test the decrypted data are in the complexity class P (for polynomial time). This means the algorithm is O(n^x), for some finite x. Inverting the function should be in the class NP (for nondeterministic polynomial time), which means we guess the key, then determine if our guess is correct in P time.]

One example is XOR, which we learned about in class. The truth table for XOR is reproduced below:

P	Q	P (+) Q
0	0	0
0	1	1
1	0	1
1	1	0

If we take P to be our input text, and Q to be our shared key, we can easily calculate P (+) Q. Just given P (+) Q though, look how hard it would be to find P - it seems impossible without knowing Q! In practice, you would convert your text to binary and your key to binary. Then you XOR the text with the key concatenated with itself enough times to match the length of the text.

This, of course, isn't perfect either - it's suspectable to frequency analysis just as codebooks are, but it's a lot harder to crack. It does form a component of many encryption algorithms used commonly though!

The algorithm I'm asking you to make doesn't need to exhibit the "one-way function" property discussed above (though it can). The algorithm should be more complex than just a basic substitution cypher, as those are very easy to break. Your algorithm should work for any size input - if I decided to test it by encrypting an entire book, I should be able to.

What you do can vary in complexity from fairly easy (using something like a code book) to things much more ambitious (asymmetric systems where different encryption and decryption techniques are used). These are all acceptable, though I'll be a bit more strict on correctness for the easier ones.